摘 要::LLC諧振電路因具有高功率密度,高效率等優點成為研究的熱點,由于其輸出電壓不是正弦交流電,研究焦點集中在直流電壓輸出的LLC諧振變換器。為了在正弦交流電源中利用LLC諧振電路的優點,本文介紹一種在LLC變換器基礎上改進的直流-交流變換器。首先在Saber仿真基礎上論證電路能實現正弦交流輸出,然后對電路進行頻域分析,并提出一種能實現軟開關的參數設計方法,最后根據所述方法設計電路并仿真驗證理論的正確性。
關鍵詞:LLC諧振,交流電源,Saber仿真
交流電源已廣泛應用于家電制造業,電子鎮流器,電機,電子制造業醫療設備等需要不同頻率電壓及特殊要求的場所。而LLC諧振變換電路因為能實現軟開通等優良特性廣泛應用于直流電壓輸出電路中。本文提出一種穩定工作情況下等效為LLC的直流-交流變換器。《中國信息化》雜志由新聞出版總署正式批準、中華人民共和國工業和信息化部主管主辦的一本國家批準創刊的唯一一份以關注工業化與信息化融合,推進信息化進程為使命的國家級信息化媒體國公開刊物。給您提供更多的科技論文范文參考
1 電路拓撲
LLC諧振拓撲如圖1所示,輸入電壓為直流電壓,開關管S1和S2互補導通,各占50%。D1和D2分別為S1和S2體二極管。Lr,Cr和Lp構成諧振網絡。

圖1 LLC諧振拓撲
Fig.1 LLC resonant topology
半橋中點a的電壓為幅值為Ui的方波,其表達式Ua為:
,
式中 T為開關管開關頻率。
將Ua進行傅里葉變換可得到:
由于電路能通過部分高頻信號,且電容Cr具有隔直作用,所以Lp兩端的電壓波形介于矩形波和正弦波之間。Saber仿真圖如圖2所示。
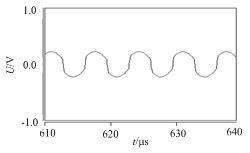
圖2 LLC電路輸出電壓仿真波形
Fig.2 Output voltage waveform with LLCcircuit
在圖1中,Lp兩端并聯電容Cp即為本文研究的電路拓撲,具體電路圖如圖3所示。在加入一定大小電容Cp后,由于存在LC低通濾波,電路的會幾乎完全阻止高頻分量的通過,加上電容Cr的隔直作用,從而使輸出為正弦波。Saber仿真圖如圖4所示。

圖3 并聯電容后的電路拓撲
Fig.3 Circuit after paralleling acapacitor
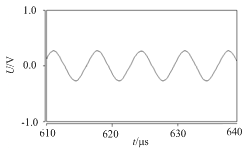
圖4圖3所示電路輸出電壓仿真波形
Fig.4 Output voltage waveform with thecircuit in Fig.3
2 電路的頻域分析
為了實現電路開關管能夠工作在零電壓導通狀態論文下載,電路總阻抗須呈感性。由于在LLC電路中并聯了電容,電路的阻抗特性與LLC電路有一定差別,下面對電路進行頻域分析。
據圖3可得電路的阻抗為:

當B>0時,電路呈感性,當B<0時,電路呈容性。但是,從上式可看出,B的值與電路中眾多參數有關,很難判別電路保持感性的條件。下面對諧振電路兩個主要部分(Lr和Cr的串聯部分,Lp, Cp和R的并聯部分)進行頻域分析。
2.1Lr和Cr的串聯部分的頻域分析
Lr和Cr的串聯部分的阻抗為:
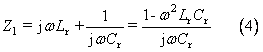
串聯諧振的頻率為:
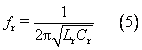
則當輸入信號的頻率f>fr時,串聯部分電路呈感性;當輸入信號的頻率ffr時等效電感為:
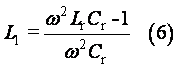
在此頻率范圍,隨著輸入信號的頻率升高,等效電感量越大,最大等效電感量為Lr,變化趨勢如圖5所示。而當輸入信號的頻率f
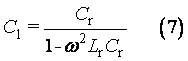
此時隨著輸入信號頻率升高,等效電容量越大,最小值為Cr,變化趨勢如圖6所示。
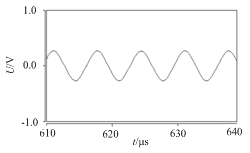
圖5 ω變化時串聯部分等效電感(電容)曲線
Fig.5 The curve of Equivalent inductance(capacitance)of the series when ω is changing
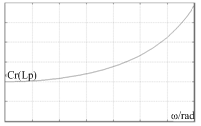
圖6 ω變化時并聯部分等效電感(電容)曲線
Fig.6 The curve of Equivalent capacitance(inductance)of the parallel when ω is changing
2.2 Lp,Cp和R的并聯部分頻域分析
Lp,Cp和R并聯部分阻抗為:

Lp,Cp并聯部分阻抗為:
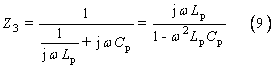
由(8)、(9)兩式可知,Lp、Cp、R并聯部分和Lp,Cp并聯部分具有同樣的容性和感性。并聯諧振頻率為:
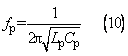
當輸入信號的頻率f>fp時,Lp,Cp并聯部分呈容性,等效電容為:
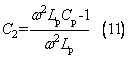
此時,當輸入信號頻率越大,等效電容量越大且最大值為Cp,變化趨勢如圖5所示。當輸入信號頻率f
此時,當輸入信號頻率越大,等效電感量越大且最小值為Lp,變化趨勢如圖6所示。
2.3電路在額定工作頻率及其鄰域的頻域分析
選取額定工作頻率f=fr,此時Lr和Cr的串聯部分阻抗為零,故要使整個電路呈感性,需Lp,Cp和R并聯阻抗呈感性論文下載,即有fr
下面對電路輸入頻率在f=fr鄰域電路的阻抗特性進行分析。
在輸入信號頻率f< fr時,串聯部分為容性,由(7)式可知,當頻率越靠近fr時,等效電容量C1越大,等效阻抗為:
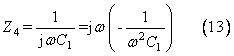
可得到1/ω2C1較小,即并聯部分只需要較小的等效電感即可讓整個電路成感性。此時并聯部分阻抗為:
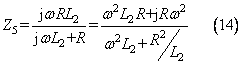
而此時并聯部分等效電感為:
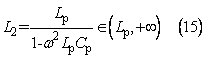
故只要L2取一個遠離正無窮和不接近零的值,并聯部分的等效電感量相對較大,可得整個電路在f
在fr
在f>fp時,并聯部分呈容性,并聯阻抗為:
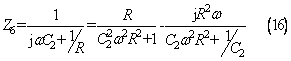
由(11)式可知輸入信號頻率f與 fp差值越小,C2越靠近零,此時
越小,即只需串聯電路有較小的等效電感,可使整個電路呈感性。由(6)式可知串聯電路等效電感為:
故當L1對零保持一定裕量時,即可得在f>fp一定區間內整個電路可呈感性。且當fp-fr越大,感性區間越大。
2.4電路可能發生的諧振
由2.1和2.2分析可知,當輸出信號頻率f從fr持續減小的時候,開始時整個電路成感性,隨著f減小,串聯部分電容性增強,并聯部分電感性增強,在假設輸出為開路的情況下,可能出現串聯部分的等效電容和并聯部分的等效電感發生諧振,會給輸出帶來高壓,此時頻率為:
在已知諧振環各參數及輸出為開路的情況下,總阻抗為0的方程可求出多個解,令其中離fr最近且小于fr的值為fa,則電路的最小工作頻率fmin應該大于fa并保持一定裕量論文下載,以免發生諧振產生高壓,或者將fa直接應用在某些需要高壓的場合。
同理,當輸出信號頻率f從fp持續增大的時候,串聯部分的等效電感和并聯部分的等效電容可能發生諧振,并帶來高壓。大部分可用于LLC諧振變換器的芯片如L6599,MC33067,NCP1396均有軟啟動功能。啟動時,變換器的頻率從一個啟動極限頻率逐漸降低。令此時極限頻率大于fp,則可利用該特性將電源用于鎮流器等場合。令此時發生諧振的頻率為fb,則:
式中C3為Cr與C2串聯的電感,即:
可得頻率為:
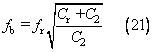
并聯等效電容C2可表示為:
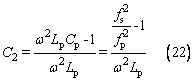
式中
。
令fs=fb,則芯片啟動時電路能輸出高壓.如果不需要該電壓,則需設計fs小于此時發生諧振的頻率fb,且保持一定裕量。
3 正常工作時電路的輸出特性
額定工作時,由于串聯部分阻抗為零,輸出電壓可近似為半橋中點電壓Ua的基波,故額定工作狀態輸出電壓為:
則功率因素校正輸出額定電壓為400V時,輸出電壓的有效值為:
=180V
當并聯部分和串聯部分均呈感性的時候,即:
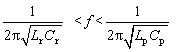
此時,隨著頻率的升高,串聯部分感抗增強,并聯部分感抗降低,故輸出電壓降低。反之,當頻率減小時,輸出電壓升高,故此特性可以用作反饋穩壓。所以可假設最高工作頻率為:
注意,這里所指的最大頻率不代表電路呈感性工作的最大頻率。此時,電路能夠通過調頻來調壓,電路工作時等效于LLC電路。
4 變換器參數的設計
經過上述分析,可以得到文中所述交流電源諧振元件參數設計方法流程圖如圖7。

圖7諧振元件參數設計流程圖
Fig.7 The flow diagram of the design ofthe resonant component parameter
5 電路仿真與總結
為了驗證本文所述方法的正確性,本文建立交流電源基于Saber的仿真模型。電路中主要參數分別為輸入電壓Ui=400V,額定功率為P=200W,輸出電壓有效值Uo=180V,工作頻率為fr=150kHz,最高工作頻率fp=200kHz論文下載,啟動頻率fs=250kHz,諧振頻率fb=300kHz,根據文中所述方法設定諧振腔各數值分別為Cr=13.2nF,Lr=84μH,Cp=8nF,Lp=80μH,fa=100kHz,最小工作頻率fmin=120kHz。得到仿真如圖8和圖9所示。其中圖8為負載為400Ω時電源的輸出電壓,圖9為負載為800Ω的輸出電壓。由仿真波形可知,輸出電壓能達到理論目標。圖10為上開關管漏源極電壓Uds和S1驅動脈沖Saber仿真波形(其中驅動脈沖電壓較小),圖11為放大后的電路波形,由圖可知,在脈沖驅動信號發生前,Uds已經下降為體二極管導通壓降,此時體二極管有向上的電流通過,即發生零電壓導通。綜上,該電源可以實現零電壓開通和正弦交流輸出,驗證了所述理論的正確性。
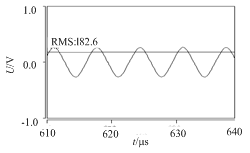
圖8負載為400Ω時電源輸出電壓仿真波形
Fig.8 Output voltage of the powerwaveform when the load is 400Ω
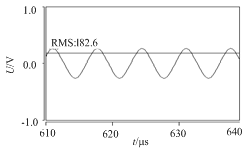
圖9負載為800Ω時電源輸出電壓仿真波形
Fig.9 Output voltage of the powerwaveform when the load is 800Ω
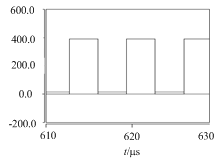
圖10Uds和S1驅動脈沖仿真波形
Fig.10 Uds and drive pulse of the S1 waveform
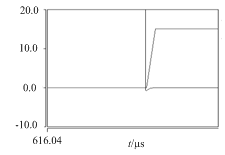
圖11圖10所示仿真圖的放大波形
論文指導 >
SCI期刊推薦 >
論文常見問題 >
SCI常見問題 >